An overview of gradient descent optimization algorithms
Sebastion Ruder의 An overview of gradient descent optimization algorithms 중 Gradient descent optimization algorithms에 집중한 글입니다. 그 외의 부분에 관해서는 위의 Sebastion Ruder의 글을 참고하시면 됩니다!


Gradient decent는 Dataset의 사용하는 규모에 따라서 위의 3가지로 나누게 됩니다.
batch(vanilla) gradient decent는 전체 트레이닝 셋에 대해 gradient을 계산합니다.
stochastic gradient decent는 sample traing set xi와 그에 대한 label yi에 대해 gradient을 계산합니다.
mini-batch gradient decent는 전체 training dataset을 batch사이즈로 나눠서 배치 셋을 순차적으로 수행하여 gradient을 계산합니다
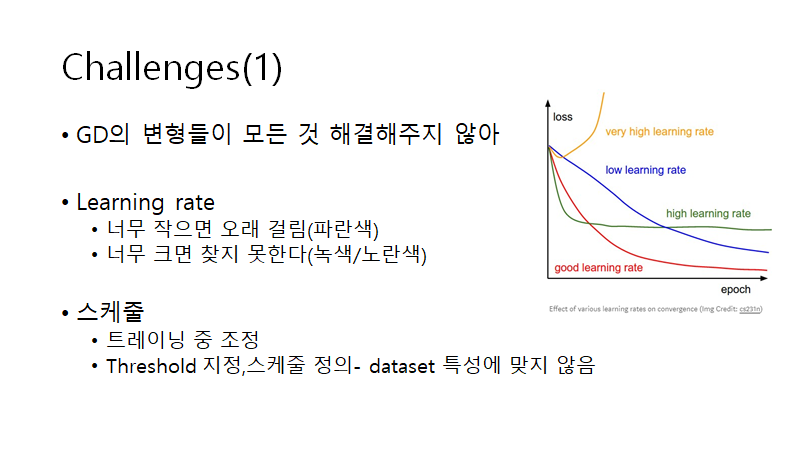
Gradient Decent의 dataset에 따른 변형들이 GD(gradient decent)가 가진 모든 문제점을 다 해결해 주진 못했습니다. GD가 직면한 몇가지 challenges가 있습니다.
첫째로 learning rate을 적절히 조절 해줘야 한다는 점입니다.
learning rate가 너무 작으면 학습속도가 너무 느리다는 점이며
너무 크면 최적의 parameter을 찾지 못할 수 있습니다.
둘째로 스케줄링 입니다. learning rate을 정해진 schedule에 따라
learning rate을 줄여주는 것입니다. 하지만, 이런 scheduling은 데이터셋의 특성상 적용하기 어렵습니다.

셋째로, 모든 파라미터들에 대해서 같은 러닝레이트를 적용하게 됩니다.
넷째로, local minima or saddle point에 빠질 위험이 있으며 이를 피해야합니다. 특히, 안장점은 모든 차원에서 gradient가 0일 가능성이 높습니다. 위의 사진을 봐도 A-B에 대해서는 minimum이지만 C-D에서는 극대값의 성질을 가지지만 검정점에서 gradient가 0에 가까워 빠져 나오기 어렵습니다.
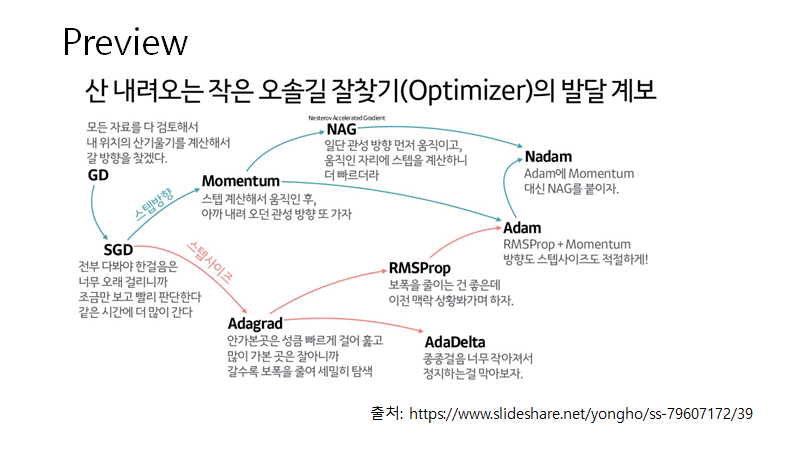
이런 challenges들을 극복하기 위해 여러가지 optimization 알고리즘들이 개발 되었는데요. 알고리즘들을 알아보기 전에 하용호님이 정리해주신 위의 자료를 보시면서 대략적인 느낌을 보시고 아랫글을 읽어보시면 개념이나 수식을 이해하는데 도움이 되실 겁니다!

첫째로, 소개된 것은 momentum이라는 개념입니다. 쉽게 말하면, 갔던 대로 더 가보자라고 생각하시면 좋을 거 같아요. SGD의 경우 위의 슬라이드의 왼쪽 아래 사진을 보시는것처럼 oscilliation에 빠지는 경우가 있는데 momentum을 적용하게 되면 기울기가 자주 바뀌지 않았던 (그림에서 보면 왼쪽에서 오른쪽으로 가는) 방향의 차원은 움직임이 커지고 기울기가 자주 변경되었던(그림에서는 위 아래) 방향의 차원은 움직임이 감소하게 되어서 더 빨라집니다.
또한, 위의 감마값은 1보다 작게(논문에서는 주로 0.9 주변의 값으로 한다고 합니다)으로 둬서 GD가 진행될 수록 예전의 gradient값들은 vanishing되게 하여 최근의 gradient가 적용될 수 있도록 합니다.
참고 : PR-042 : Adam: A Method for Stochastic Optimization
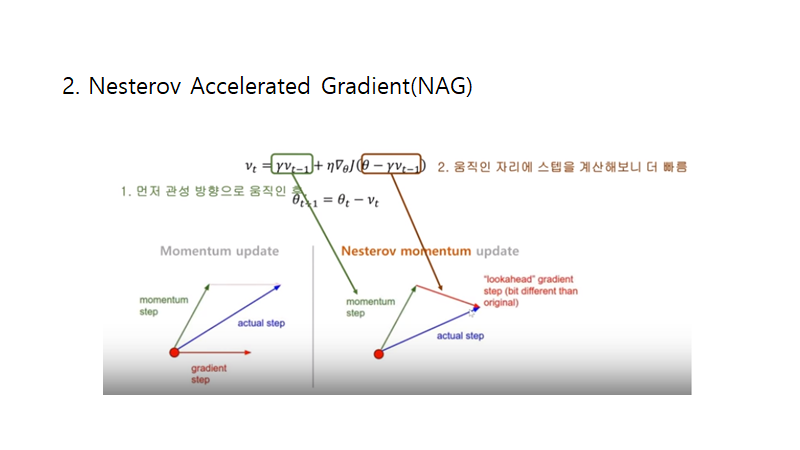
2번째로 소개된 것은 Nesterov Accelerated Gradient입니다. 위의 자료에서 엄청 쉽게 설명을 해주셨는데요. gradient decent을 계산할 때 일단, 전에 움직였던 만큼을 감마값을 곱한 후 움직이고, 그 이후 거기서 gradient을 계산하는 방법입니다. 위에서 소개한 momentum과 비슷한 개념인데 비교 해보면

모멘텀을 가리키는 것은 파란색 선,
NAG을 가리키는 것은 황색선과 빨간선 그리고 그 둘이 합쳐진 초록선입니다.
NAG는 momentum에 비해 빠르게 가는 것을 방지해주면서 RNN의 performance 향상 시켜줬습니다.

이제는 learning rate을 조정하는 알고리즘을 알아보겠습니다.
adagrad는 learning rate을 parameter별로 조정하고자합니다.
기존 GD식에다가 learning rate에 gradient을 나눠주면서 gradient가 높았던 곳은 learning rate을 줄여 세밀히 보고자하고 gradient가 낮았던 곳을 그에 비해 빠르게 움직이게 합니다.
이 알고리즘은 sparse한 데이터에 유리하다고 합니다.
약점은 수식에서 보듯 Gt가 학습이 됩에 따라서 값이 커지게 되는데
이는 learning rate에 나눠지게 되어 결국 learning rate가 줄어들게 만들어 학습이 어려워지게 만듭니다.

Adagrad의 약점을 보완하고자 여러 알고리즘이 나오는데 그 중 RMSprop은 learning rate가 없어지는 것을 방지하고자 했습니다.
- 정정) 감마값은 0.9 learning ratesms 0.001이 가장 좋은 default값이라고 제안했습니다.
AdaDelta 또한 learning rate의 Adagrad의 vanishing을 막고자 발전한 알고리즘입니다. 위의 알고리즘의 설명은 이 링크의 (18분 29초부터)로 대신합니다.

그리고 많이들 이용하시는 Adam입니다. Adam의 개념은 Momentum의 gradient 움직임과 Adagrad(Rmsprop)의 learning rate조정을 합쳤다고 생각하시면 됩니다.
first momentum
mt - gradient(gt)의 조정을 위해 momentum의 개념(과거의 움직임반영)
second momentum
vt - learning rate의 조정을 위해 RMSprop의 learning rate 조정 개념
하지만, 초기 m,v값이 0으로 초기화 되어 있어 mt와 vt 값이 0에 가깝게 bias되어있을 것을 판단하여 이를 보정하는 식을 거쳐서 이를
parameter 조정 하는 세번째 식에 대입하여 계산한다.
그리고 Adam의 발전된 혹은 일반화 된 모형들이 소개됩니다.
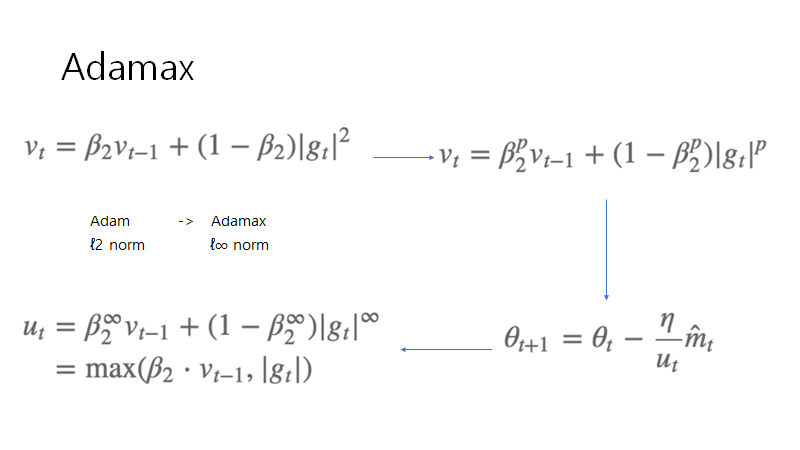
정정) 위의 그림에서 위의 오른쪽에서 아래의 오른쪽으로 가는 화살은
위의 오른쪽 식에서 아래 왼쪽의 식로 진행되고 그 후 오른쪽 아래의 식으로 진행됩니다.

Nadam은 Adam의 momentum 개념을 NAG개념으로 대신합니다.

출처 : 참고
위의 표를 통해서 알고리즘들이 gradient decent의 어떤 부분을 조정 하고자 했는지 그리고 각 알고리즘 별로 논문들의 저자들이 제안하는 hyperparmeters의 추천 값을 정리합니다.

저자는 위에서 제안된 optimizer중 어떤 것을 선택해야하는 질문에
Adam might be the best overall choice라고 합니다만 이와 같은 논문에서는 RMSprop이 우수하다고도 전달합니다.
많은 논문에서 vanilla SGD을 모멘텀과 adaptive learning rate 혹은 스케줄링 없이 이용하지만, 이는 앞서 말한 gradient decent가 직면한 challenges에 직면하게됩니다.
그래서 저자는 복잡한 신경망을 이용하는 경우 adaptive learning rate method(Adagrad에서 파생된 알고리즘)을 사용해야한다고 합니다.
부족한 글을 봐주셔서 감사합니다.
글에서 수정해야할 사항이 있다면 알려주시면 감사하겠습니다!
