List을 통해 구현해본 Sparse Matrix
Linked-List 개념과 코드 구현 : 링크
이번 글에서는 리스트를 응용해서 Sparse Matrix에 대해 이해하고 구현해 본 것을 소개드리고자 합니다.
Sparse Matrix란?
행렬의 값이 대부분인 0인 경우를 가리키는 표현
텍스트 데이터를 다루시는분들이라면 한번쯤 보셨을 만한 TDM(Term Document Matrix)가 바로 희소행렬을 활용한 대표적인 예입니다.
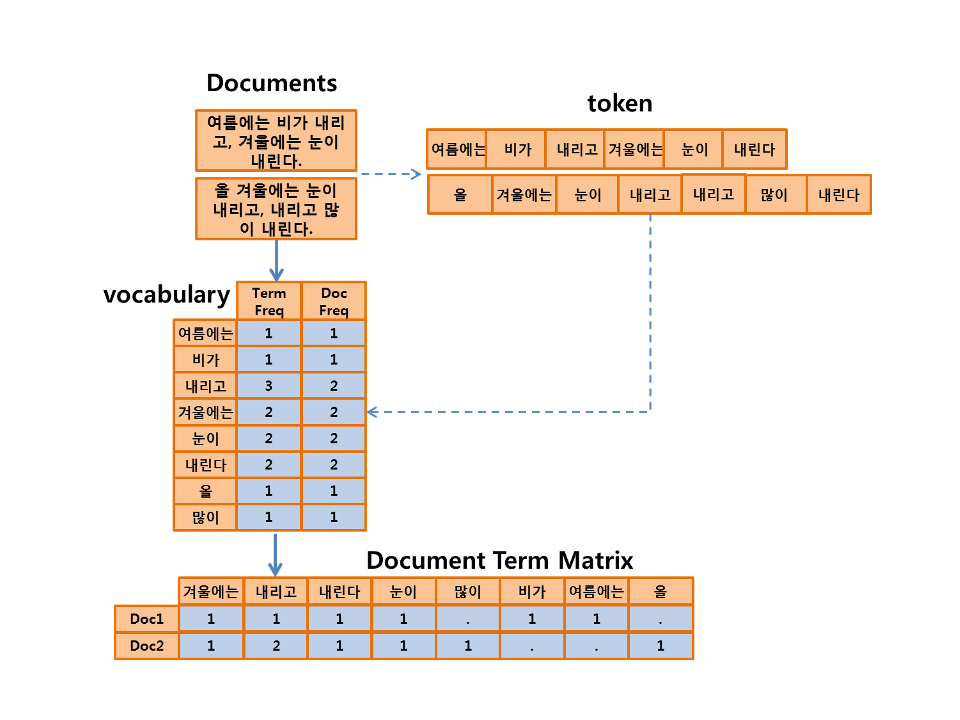
출처 : xwMOOC
문서를 vectorization연산이 가능하게 하기 위한 구조로 변환 하기위한 과정입니다.
주로 이용하는는 방법은 한 document안에 위 단어가 있는지 혹은 얼마나 있는지를 행렬로 표현하는데요
Document가 늘어나면 쓰이는 단어도 많아져서 위의 그림을 보시게 되면 컬럼이 많아 질 것이고 0인 값을 가지는 셀도 많아질 것입니다.
결국 DTM(희소행렬)을 저장 할 때, 0도 값(cost)이기 때문에 메모리를 차지합니다.
이를 해결 하기위해서 TF-IDF와 같은 cut-off을 설정하여 column수를 줄이거나 n-gram을 활용하는 방법들이 주로 사용됩니다.
그럼에도 불구하고, 0인 값들을 저장하는 것은 효율적이지 않으므로 이를 효율적으로 저장하기 위한 자료구조를 생각해봅니다.
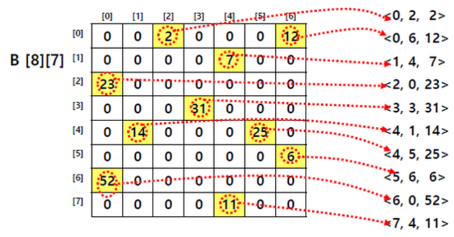
- SparseMatrix 자료구조
- init : 행렬의 dimension m, n 을 입력받아 희소행렬 리스트를 [[m,n,0]]로 초기 설정한다.
- append method: [i, j, value] 형태의 리스트를 희소행렬 리스트에 추가한다.
- shape method: 희소행렬 dimension을 리턴한다.
- getValue method: i, j 행렬값을 리턴한다.
- print method: 희소행렬을 일반적 행렬 형태로 프린트한다. (0으로 구성된 m,n array를 만들고 i,j 행렬값을 업데이트한다.)
class SparseMatrix:
def __init__(self, m, n):
self.s = [[m, n, 0]]
self.m = m
self.n = n
def append(self,i,j,val):
if val != 0:
self.s.append([i,j,val])
# s[0][2]에는 DTM에 몇 개의 값을 가진 셀이 있는 지 보여줌
self.s[0][2] = len(self.s) - 1
def shape(self):
return (self.m, self.n)
def getValue(self, i, j):
val = 0
for k in range(1,len(self.s)):
if self.s[k][0] == i and self.s[k][1] == j:
return self.s[k][2]
return 0
def print(self):
import numpy as np
_tmp = np.zeros((self.m, self.n))
for i in range(1,len(self.s)):
_tmp[self.s[i][0]-1,self.s[i][1]-1] = self.s[i][2]
print(_tmp)
EX) 3*3행렬 생성
a = SparseMatrix(3,3)
b = SparseMatrix(3,3)
a.append(1,1,1)
a.append(2,2,2)
a.append(3,3,3)
b.append(1,1,4)
b.append(1,2,7)
b.append(2,3,2)
b.append(3,3,1)
a.print()
b.print()
print(a.getValue(3,3))
희소행렬의 전치행렬 알고리즘 : 희소행렬의 행 [i,j,val] 을 [j, i, val] 로 바꿔 리턴한다.
두 희소행렬의 덧셈 알고리즘:
- 덧셈 결과를 저장할 빈 희소행렬 c를 만든다.
- 두 희소행렬 a, b의 unique 한 (i,j) 쌍의 집합을 u 라고 하자.
- u에서 원소를 하나씩 꺼내면서 a, b의 해당 위치 값을 구해 더한다.
- 위에서 구한 값이 0이 아니면 c에 추가한다.
def transpose(a):
#행과 열의 값을 바꿔서 저장
t_a = SparseMatrix(a.n,a.m)
# 첫번째 값은 그대로 몇개가 들어있는지
# 그외에는 행과 열의 값을 바꿔서!
for i in range(len(a.s)):
if i == 0:
t_a.s[0][2] = a.s[0][2]
else:
t_a.append(a.s[i][1],a.s[i][0],a.s[i][2])
return t_a
# EX
t_b = transpose(b)
t_b.print()
def add(a, b):
if a.shape() != b.shape():
print("두 행렬의 차원이 달라 더할 수 없습니다.")
else:
c = SparseMatrix(a.shape()[0], a.shape()[1])
u = set()
for i in range(1,len(a.s)):
u.add((a.s[i][0], a.s[i][1]))
for i in range(1,len(b.s)):
u.add((b.s[i][0], b.s[i][1]))
for item in u:
_tmp = a.getValue(item[0], item[1]) + b.getValue(item[0], item[1])
if _tmp != 0:
c.append(item[0], item[1], _tmp)
return c
# EX
a.print()
b.print()
c = add(a, b)
c.print()
위와 같이 Sparse Matrix을 구현해봤습니다.
TDM은 어떻게 구현이 되는 지 보고싶은 분들은 sklearn의 CountVectorizer source에서_count_vocab을 참고하시면 좋을 것 같습니다!
